A STEM Project: The Beauty of Coding Koch Snowflakes In TurtleStitch

A Koch Snowflake

This snowflake fractal design was discovered by Helge von Koch, a Swedish mathematician in 1904. It was one of the first fractal designs to be described. A fractal is a design whereby a part of the design has the same characteristics as the whole. This snowflake fractal design is also known as a recursive design because in the coding of the program, the design block calls itself. The result is a smaller version of itself.

In 1905, Italian mathematician, Ernesto Cesaro eloquently described the self similarity of the Koch snowflake as following...

“It is this similarity between the whole and its parts, even infinitesimal ones, that makes us consider this curve of von Koch as a line truly marvelous among all. If it were gifted with life, it would not be possible to destroy it without annihilating it whole - for it would be continually reborn from the depths of its triangles, just as life in the universe is.”

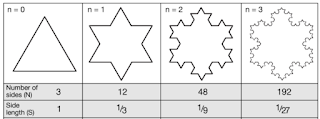
Constructing A Koch Snowflake

 1). Take a straight line and divide it into three equal parts. 

 2). Replace the center with two sides of an equilateral triangle. 

(This is the self similarity that gets repeated in all levels.)

 3). Replace each side of design in step #2 with the self similarity.

Notice there are four repeats of this design which are 1/3 the size of the original self similarity.

To make this design into a Koch Snowflake, repeat the design in step #3 and turn the design by 120 degrees three times to complete the circumnavigation. 

The result is a Level 2 Koch Snowflake.

 To make a Level 3 Koch Snowflake, repeat the replacement of the self similarity in step #3 and turn the design in the same manner as before. 

 Each self similarity will be one-third the size of the previous side length.

Coding A Koch Snowflake In TurtleStitch

Here is my code

https://www.turtlestitch.org/run#cloud:Username=Elaine&ProjectName=Koch%20Snowflake

The diagram above shows  five iterations of the fractal design drawn with a recursive block called "kochcurve". The first figure represents level 0 in the recursive program (or stage 1 according to Koch's paper). The next figure represents the next level/stage and so on. This program can be repeated forever. The general size of the snowflake will alway remain the same but the size of the self similarity becomes almost infinitesimal.              

Here is the TurtleStitch code for the generalized block named “kochcurve” which produces the different levels of a Koch Snowflake. 

When the ‘kochcurve’ is executed with the parameters for side length of 100 and level # of 0

The result is a straight line.

Since only one side of the snowflake is produced, a turn of 120 degrees must be added. This code is then repeated 3 times to complete the entire Koch Snowflake figure.

The result of the code is a triangle.

When the ‘kochcurve’ is executed with the parameters for side length of 100 and level # of 1, the result is the figure below.

Again, since only one side of the snowflake is produced, a turn of 120 degrees must be added.

This code is then repeated 3 times to complete the entire Koch Snowflake figure.

The result of the code is a six point star.

When the ‘kochcurve’ is executed with the parameters for side length of 100 and level # of 2

The result is the figure below.

Again, since only one side of the snowflake is produced, a turn of 120 degrees must be added. This code is then repeated 3 times to complete the entire Koch Snowflake figure.

The result of the code is the snowflake below.

Coding A Koch AntiSnowflake in Turtlestitch

The above snowflake is a level 3 Koch Antisnowflake.  It was coded in TurtleStitch with a "turn 120 degrees" to the left instead of "turn 120 degrees" to the right. Here is the code for the Antisnowflake, https://www.turtlestitch.org/users/Elaine/projects/Koch%20AntiSnowflake

The diagram above shows  five iterations of the Antisnowflake. It is interesting to see that the self similarity of the Antisnowflake remains inside the original triangle as its size decreases each time by one-third.

Comparing the above diagram with the five iterations of the original Koch Snowflake, the self similarity of the Koch Snowflake remains outside the original triangle design as its size decreases each time by one-third.

Two Projects to Make With the Koch Snowflake

A Koch Snowflake Ornament

A Koch snowflake ornament was made in TurtleStitch using four levels of the Koch snowflake design. Level 1 is in the center and each subsequent snowflake is the next level up to level 4. A satin stitch was coded around the entire design with a circle at the top for a hanger.

This Koch Snowflake Ornament can be found at

https://www.turtlestitch.org/users/Elaine/projects/Koch%20Snowflake%20Ornament

Craft felt with tear away stabilizer was used as backing for the design.  Once embroidered, the design was cut about an ⅛ inch from the satin stitch.  It is not recommended to cut any closer to the satin stitch, as a slip of the scissors might cut the satin stitch threads. A bow and a thread hanger were sewn on to complete the snowflake ornament.

Making a Snowflake 

Ballerina out of a Koch Snowflake

The ballerina design was traced in TurtleStitch. (To learn more about tracing in TurtleStitch, visit this blog posting. https://papercraftetc.blogspot.com/2022/03/a-stem-project-coding-in-turtlestitch.html ) 

The snowflake is a level 4 Koch Snowflake.

The ballerina and snowflake were exported as a DXF file to a paper cutting machine like a Silhouette and cut out from 65 lb. cardstock.

Here is the TurtleStitch program to make the Koch Snowflake Ballerina: https://www.turtlestitch.org/run#cloud:Username=Elaine&ProjectName=Koch%20Snowflake%20Ballerina

Once the Koch Snowflake was cut out, pleats were added in the snowflake for interest. The Koch Snowflake was then slipped over the ballerina to resemble a frilly tutu.

FYI...In a previous blog posting, I made these snowflake ballerinas by cutting out the snowflakes (not Koch snowflakes) by hand. https://papercraftetc.blogspot.com/2013/12/when-it-snows-make-christmas-ornaments.html